Loops and Conditionals
In this lab, we’ll continue our exploration of loops and introduce a new concept that will allow us to make even more interesting drawings: conditionals.
Intro to conditionals
One of the most powerful ways to utilize computation is to respond to differences in the context our code is running in by changing the behavior of our code. This might sound complicated, but as a human you are very familiar with this kind of response.
Conditional behavior
There are many situations where you change your behavior based on the environment. For example, if it is raining outside, you wear rain boots. Otherwise, you might wear a different kind of shoe like tennis shoes.
You probably have even more complicated environmental responses as well. For example, if you are ordering bubble tea, your order might go like this: if the shop has taro, you get taro in your tea. If the shop doesn’t have taro but has pearl, you get pearl in your tea. Finally, in the case that the shop doesn’t have taro or pearl, you don’t order any bubble tea.
In computer science, we call this kind of behavior conditional: your code runs only in the case that some condition is satisfied.
Conditions
In computer science, conditions are binary. They are either true or false, never inbetween. To create these conditions, we can use comparison operators to compare values.
💻 Guess what condition the following comparisions will evaluate to. You can test your guesses by typing these conditions into the Python shell:
2 < 3
2 == 3
"Gold" == "Silver"
"Gold" == "Gold"
Python has the following comparison operators: <, >, ==, <=, >=, !=.
✏️ Using the Python shell to experiment, create a table like the one below that defines what each of the operators does and gives an example of when the operator will generate a True condition and when the operator will generate a False condition:
| Operator | Description | True condition example | False condition example |
|---|---|---|---|
< |
|||
> |
|||
== |
|||
<= |
|||
>= |
|||
!= |
Conditionals
Using the conditions generated by comparison operators, you can conditionally execute pieces of your code. This is useful for changing what your code does to respond to different condtions of the program.
if statements
if statements are the begining to every conditional code block. The code written inside the code
block that follows only runs if the condition after the if evaluates to True.
for i in range(20):
if i < 10:
print("Smaller than 10")
else statements
else statements can be paired with if statements to create an alternative block of code to
execute if the condition after the if evaluates to False.
What is the difference between the following two programs?
for i in range(20):
if i < 10:
print("Smaller than 10")
print("Greater than or equal to 10")
for i in range(20):
if i < 10:
print("Smaller than 10")
else:
print("Greater than or equal to 10")
elif statements
Finally, elif statements (“else if”) can be used to create multiple branches of a conditional.
These statements add another condition to check if the condition above them does not pass.
The following program creates three branches of exectution:
for i in range(20):
if i < 10:
print("Smaller than 10")
elif i < 15:
print("Greater than 9 but less than 15")
else:
print("Greater than or equal to 15")
This conditional creates the folloing cases for the variable i:
- i < 10
- 10 <= i < 15
- 15 <= i
A. Responding to user input
One way to use conditionals in our drawings is to use them to respond to user input.
💻 Create a new file in your cs9/unit_00 directory called lab_03.py
and paste in this starter code:
# A. USER INPUT
from turtle import *
speed(10)
while True:
drawing = input("What would you like me to draw? ")
size = int(input("How big should I draw it? "))
if drawing == "square":
for i in range(4):
forward(size)
right(90)
elif drawing == "quit":
break
else:
print("Sorry, I don't know how to draw that...")
💻 Run this program to see how it uses a conditional based on user input.
This program has a lot of potential, but so far it can only generate one drawing.
💻 Add at least two more branches to the conditional so that the program can
draw more shapes. An elif statement will probably be useful here.
✅ CHECKPOINT:
Answer the following check-in questions on your group’s Google doc before moving on:
- What is the difference between
elseandelifstatements in a conditional?- When writing a conditional, what kinds of things can you compare? Can you compare different types of things to each other?
Modulo
Python has many operators that allow you to perform calculations with values. You’ve probably
seen and used the basic ones like +(add), - (subtract), * (multiply), and / (divide).
However, Python has some other less common opertors that can be really helpful.
One such operator is the modulo operator (%). This operator takes two values, divides them,
and returns the remainder of the division. Try out the following operations using modulo to
get an idea for how it works:
| Calculation | Result |
|---|---|
5%3 |
|
3%3 |
|
6%2 |
|
0%6 |
|
5%0 |
B. Rainbow
Conditionals can also be paired with the modulo operator to cause your code to run in repeated patterns.
💻 Copy the code below into your lab_03.py file and run it to see what it does,
# B. RAINBOW
speed(10)
for i in range(5):
color("red")
begin_fill()
for j in range(4):
forward(100)
right(90)
end_fill()
penup()
right(45)
forward(10)
left(45)
pendown()
color("orange")
begin_fill()
for j in range(4):
forward(100)
right(90)
end_fill()
penup()
right(45)
forward(10)
left(45)
pendown()
color("yellow")
begin_fill()
for j in range(4):
forward(100)
right(90)
end_fill()
penup()
right(45)
forward(10)
left(45)
pendown()
color("green")
begin_fill()
for j in range(4):
forward(100)
right(90)
end_fill()
penup()
right(45)
forward(10)
left(45)
pendown()
color("blue")
begin_fill()
for j in range(4):
forward(100)
right(90)
end_fill()
penup()
right(45)
forward(10)
left(45)
pendown()
color("purple")
begin_fill()
for j in range(4):
forward(100)
right(90)
end_fill()
penup()
right(45)
forward(10)
left(45)
pendown()
color("violet")
begin_fill()
for j in range(4):
forward(100)
right(90)
end_fill()
penup()
right(45)
forward(10)
left(45)
pendown()
input()
This code is really long. However, there is a pattern to the rainbow that we could use to simplify the code: the rainbow has 7 colors that repeat every time the loop runs for 7 iterations.
💻 Simplify this code using a conditional and the modulo operator.
✅ CHECKPOINT:
Answer the following check-in questions on your group’s Google doc before moving on:
- How would you describe the modulo operator to a friend who has never heard of it before?
- What other situations do you think the modulo operator would be useful in?
While loops
In addition to for loops which run for a set number of iterations, Python has another type
of loop. while loops iterate until a particular condition is met.
Conditions
while loops use conditions just like if statements. You can use operators to compare
values in or to generate True or False conditions. Looping until a condition is met
can be useful when you are getting getting input from a user, generating random variables,
or repeatedly applying a transformation to a value.
user_input = -1
while user_input < 1 and user_input > 10:
user_input = input("Tell me a number between 1-10 (inclusive): ")
While True / Break
You can also make while loops run indefinitetly by setting the condition to True like
this: while True:. This can be useful when you want to loops a program repeatedly.
To stop a loop like this, you can use a break statement. Once the program reaches the
break, the loop will exit.
You’ve actually already seen an example of this kind of loop at the beginning of the lab.
speed(10)
while True:
drawing = input("What would you like me to draw? ")
size = int(input("How big should I draw it? "))
if drawing == "square":
for i in range(4):
forward(size)
right(90)
elif drawing == "quit":
break
else:
print("Sorry, I don't know how to draw that...")
C. Hailstone sequence
In the last part of this lab, you will be exploring a special sequence known as the hailstone sequence. This sequence results from the following rules (known as the Collatz conjecture):
- take any positive number
n - find the next term of the sequence using the following rules:
- if
nis even, the next term isn/2 - if
nis odd, the next term isn*3+1
- if
- repeat until
n = 1
The conjecture states that no matter the starting value of n, the sequences will always
reach 1.
✏️ Try this out: pick a number and perform the calculations. Can you find a number that doesn’t reach one?
This sequence is interesting because though no number has ever been found that doesn’t reach 1, the Collatz conjecture has never been proven. This is an unsolved problem in mathematics!
C.0 Calculating hailstone sequences
Pseudo-code
This is another alogrithm which will require pseudo-code to figure out. ✏️ Write out pseudo-code to plan the logic of this program.
Here are some things to consider:
- This program will require a loop. What kind of loop do you think is best? Remember that for loops run for a definite number of times and while loops run until a condition is met.
- You will need to determine if each term is odd or even. What are some characteristics of even numbers that will help you determine if a number is even?
- In addition to calculating each term, you should also count how many steps it takes to
reach zero and report this number at the end. You should use a
countvariable to track the number of steps.
Code
Once you’ve completed your pseudo-code, you can translate it into Python code.
💻 Use the following to get started:
# HAILSTONE
num = int(input("What number should I calculate the hailstone sequence of? "))
# Put your code here
print("Took " + str(count) + " steps to reach 1.")
✅ CHECKPOINT:
Answer the following check-in questions on your group’s Google doc before moving on:
- What kind of loop did you choose to write the hailstone sequence algorithm? Why did you choose this kind of loop?
- Why do you think the Collatz conjecture is so hard to prove for all positive integers?
C.1 Drawing Hailstone
The sequences formed are known as hailstone sequences, because the terms move up and down but ultimately reach 0 like hailstones gaining layers of ice in a cloud.

Hailstones froming in a cloud
This pattern can lead to some interesting visualizations of hailstone sequences.
You can visualize the terms in a sequence starting with a specific number:
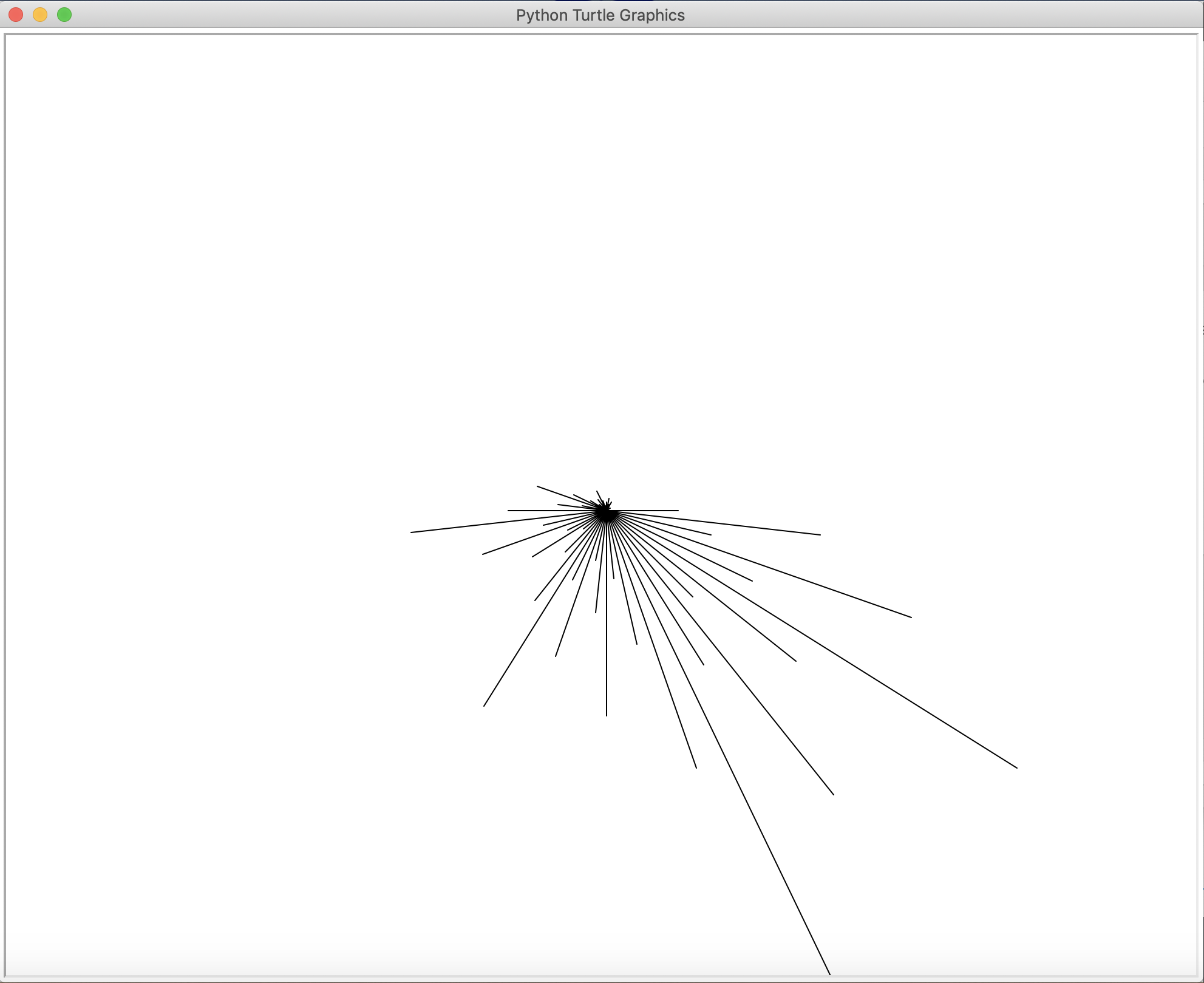
Terms in hailstone sequence starting at 590
Or you can visualize the number of steps it takes to reach one from a set of integers:
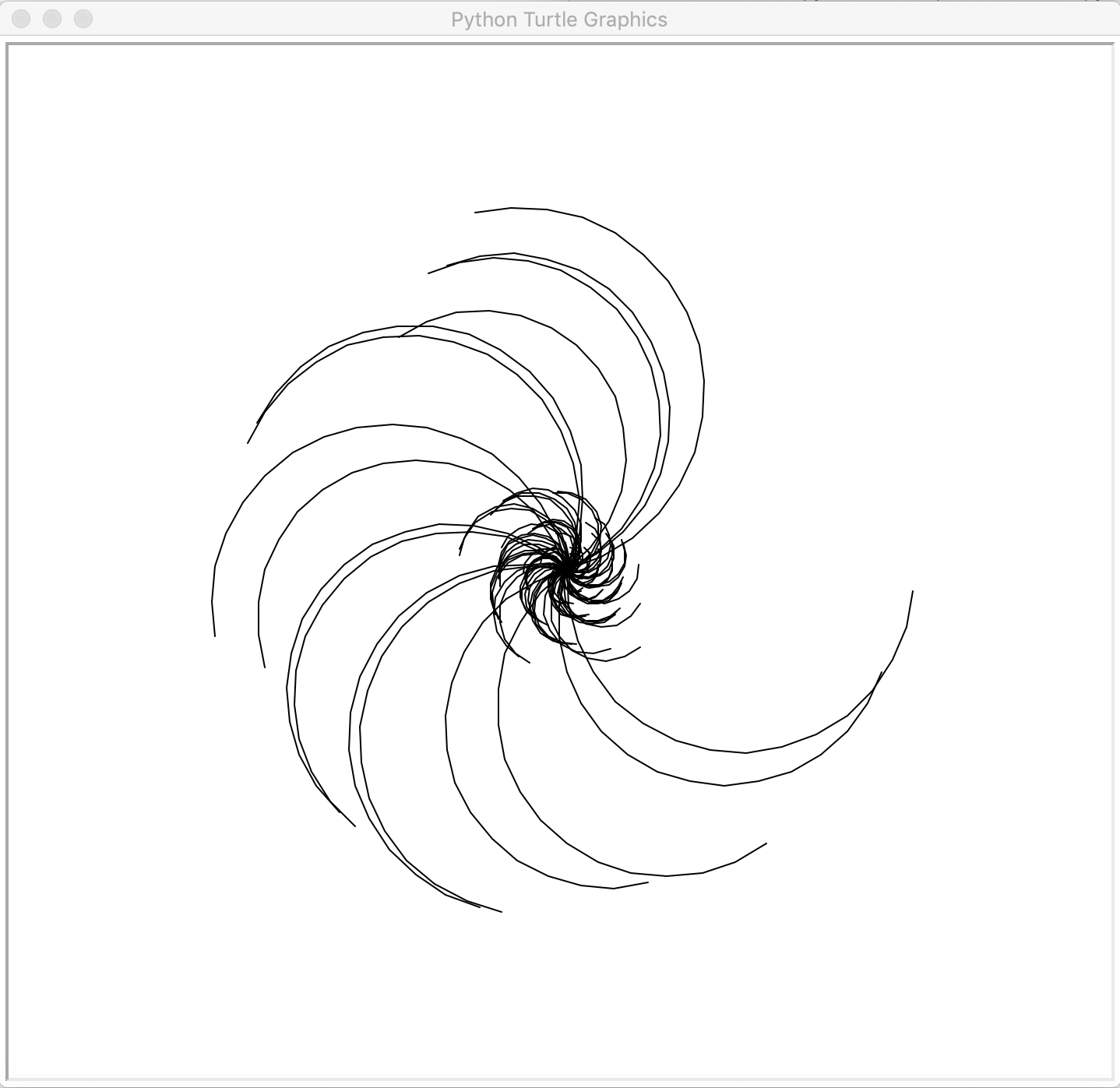
Steps to reach one in hailstone sequence as radii of half circles for integers 1-100
💻 Use your hailstone sequence code from part C.0 to create a visualization fo the hailstone sequence using Turtle.
Deliverables
For this lab, you should submit the following:
- The your
lab_03.pyfile with the code you wrote for each of the parts - Your Google Doc with responses to the checkpoint questions